

1.金融・投資の世界で言うリスクとは?
投資と聞くとついつい儲け、、、いわゆる”リターン”に目が行きがちですが実際問題はというと、リスクはある程度自分で管理できるのに対してリターンはそれが不可能です。
そのため投資ではリターンに目をやるのではなく”リスクの管理”が最も重要だと言われています。
金融に関する数学的な理論を学ぶ学問で
金融工学
というものがあるのですが、そんな金融工学の柱と言われるものに以下の2つがあります。
- 1つがデリバティブという金融派生商品の価格決定理論
- もう1つが今回のテーマであるリスク管理を支える理論
です。
ちなみに以前にブログで市場の将来予測は不可能といった内容を書きましたが、この“予測は不可能”というのも金融工学の基本とされています。
そのため、投資をする際にはまずはこの”リスク”について知っておくことは基本であり必須になってきます。
今日はそんなリスクについて簡単に触れていきます。
早速ですが、、、
それではその金融、投資の世界で言うリスクとは何なのでしょうか。
結論を先に言うとそれは
平均からのリターンのばらつき具合
をリスクと表現します。
どういうことかというと、皆さんも
- ハイリスク・ハイリターン
- ローリスク・ローリターン
という言葉を聞いたことはないでしょうか。
言葉通りですが
ハイリスク・ハイリターンとはいわゆる大きく儲けるか、大きく損をするか、
それに対して
ローリスク・ローリターンとは損をするのは小さいが儲けも小さい
ことを意味します。
これに集約されているといっても良い気がしますが、基本的に大きく儲けるなら大きく損をする覚悟が必要ですし、大きな損をしたくないのであれば儲けも小さくなることを受け入れなければなりません。
これは投資経験の有無に関係なく肌感覚的にもある種当たり前のような感じがしますがリスクとリターンは表裏一体の関係になります。
大きなリターンを得たいのであればリスクも許容しないといけませんし、逆にリスクを負いたくないのであれば大きなリターンは期待するべきではありません。
ではそのリスクに関してもう少し具体的に表現するとどうなるでしょうか。
実はリスクは標準偏差で表されます。
統計学で出てくる用語ですがおさらいすると
- 平均からの乖離を“偏差”
- その偏差を2乗して相対度数をかけたものの和を“分散”
- その分散の平方根をとった値を“標準偏差”
と言います。
(相対度数とはある値が全体に占める割合を表した数を指します。)
今思えば私は短大、専門学校、大学の全てで統計学を履修していたので授業で全部これが出てきましたが初めて見た時は何のためにあるんだと思っていました(笑)。
この標準偏差の意味はというと“ばらつきの大きさ”を表しています。
標準偏差の数値が大きければそれだけ”ばらつき”が大きいことを意味し、イコールでリスクが高いと考えられます。
例えば現在大手金融機関の定期預金金利は0.001%~0.002%程度ですが、これは元本と利払いは銀行が保証しています。
そして単純に考えて仮に0.001%の金利であれば100万円預けている場合は1年後に10円の利息がつきます。
この際の1年後のリターンは“確実”であり10円以上になることもなければそれ以下になることもありません。
つまり”ばらつき”のない状態、、、リスクゼロの投資であると言えます。
預金にリスクがないと考える方も多いと思いますが、この預金に何故リスクがないのかと言うと“ばらつきがないため”と言えます。
余談ですが、預金は確かにある一定金額まで銀行が倒産しようと預金保険制度で元本は保証されていますし当然ながら預金額が減ることもなく”ばらつき”というものはありません。
(しかし、だからといって預金がノーリスクかと言えば実はそうとも言えない面もありますが話が逸れてしまうのでその点についてはまた別の機会に書きたいと思います。)
ではなぜそんなにリスク、、、いわゆる”ばらつき”が重要なのでしょうか。
一言で言うとこの標準偏差によって、同じ数値であってもその数値の意味が変わるためと言えます。
少しイメージしやすいように例を挙げたいと思います。
2.学校の偏差値も標準偏差を使っている?
リスクは標準偏差であるとしましたが、標準偏差の説明でよく使われるものとして学校のテストの「偏差値」があります。
皆さんも模試や学校のテストで見たことあると思いますが、偏差値は言葉通りこの標準偏差を使ったものとなります。
そしてその偏差値は以下の式で表すことができます。
「偏差値=(自分のテストの点数-平均点)÷標準偏差×10+50」
ちなみに平均点は馴染みがあるので、平均点の求め方は各点数を足してその総数をテストを受けた人数で割って求めることはご存知だと思いますが数学的に表現すると以下のようになります。
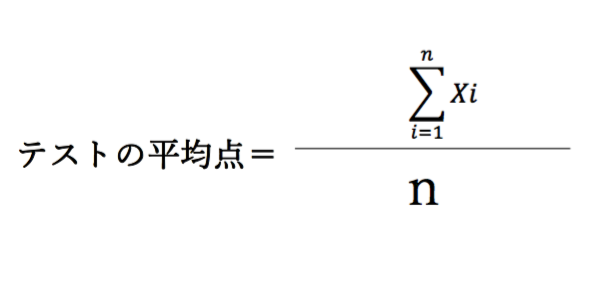
こうした記号がでると嫌な方も多いかもしれませんが、私も文系なのでお気持ちはわかります(笑)
高校数学をお忘れの方もいるかもしれないので補足を入れると、まずΣ(シグマ)は総和を意味します。
“n”は人数を表しており、“x”は個別の点数、“i=1”は初期値が1であることを意味し、1からnまでを足し合わせるといったことを表しています。
慣れないと難しいかもしれませんが、普段何気なく平均点を出している方法を数学的に表現するとこうなるといっただけです。
要するに個別の点数を足し合わせた総数をn(人数)で割っているというのを表記を変えて表現しているだけになります。
そして同様にテストの標準偏差は

で求められます。
ここで仮に平均点が50点だったテストについて考えてみます。
そしてそのテストには2種類あり、
- 1つが標準偏差が20のテスト→Aテスト
- もう1つは標準偏差が40のテスト→Bテスト
とします。
仮にこの各テストで100点をとった人と0点をとった人の偏差値を比べてみるどうなるでしょうか。
実際に計算してみると、
- Aテスト(標準偏差が小さい):100点→偏差値75、0点→偏差値25
- Bテスト(標準偏差が大きい):100点→偏差値62.5、0点→偏差値37.5
となります。
同じ点数でもBテストでは100点をとってもAテストと比べて偏差値が低いことがわかります。そして反対に、Bテストでは0点をとったとしても偏差値はAテストよりだいぶ高いことがわかります。
Aテストと比べてBテストでは高い点数をとってもAテストほど偏差値が高くならない。
かといって同じBテストでは0点をとってもAテストほど偏差値は低くもならない。
なんとなく「ん?」と思うかもしれませんが、これはグラフにしてみるとわかり易くなります。
AテストとBテストの違いは標準偏差の違いです。そして、標準偏差とは数字のばらつき具合を示すことを紹介しました。Bテストは標準偏差が大きい、、、いわゆるテストの点数の結果のばらつきが大きいことを意味しています。
それをグラフにすると以下のようになります。
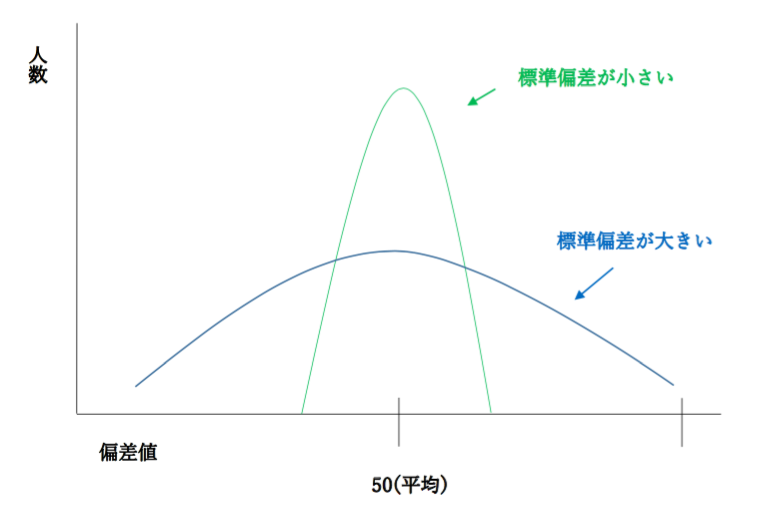
縦軸に人数、横軸が偏差値となっており、先ほどの例えで言うとAテストが緑色のグラフにあたり、Bテストが青色のグラフにあたります。
見ての通り、標準偏差が小さいとは数字のばらつきが小さいこと、、、テストにおいて言うとみんなのテストの結果が平均点あたりにまとまっていることを意味します。
平均点あたりにまとまっているということは言い換えれば、そこから離れている0点や100点といった点数は両方とも珍しい数値であり希少であることになります。
そのためAテストのような標準偏差の小さいテストであれば、平均点から離れた点数結果は希少性が高くなり、Bテストと比べて高偏差値・低偏差値が発生することになります。
逆にBテストでは、元々テストの結果のばらつきが大きいため極端な点数である0点や100点をとったところでAテストの時ほど希少性は少ないものとなり、高偏差値や低偏差値はAテストより出にくくなります。
そのため同じテストの点数結果であったとしても、標準偏差の違いによりその意味が変わってくることがわかります。
3.金融の世界で言うリスクのおさらい
なんとなく標準偏差のイメージがつかめましたでしょうか。
ここで最初の話に戻りますが、金融の世界では”ばらつき具合”をリスクとしており、そのリスクは標準偏差で表されると紹介しました。
改めて振り返ると、これは言葉にするとどういうことなのでしょうか。
先ほどは偏差値だったのでテストの点数としていましたが、例えば投資で例えるとこのテスト結果である点数の代わりに入るのは、投資の結果、簡単に言えば利益(リターン)となります。
いわゆる投資のリターンのばらつき具合が少ない(標準偏差が小さい)グラフとは、投資結果がそれだけ平均近くに収まる可能性が高いことを意味しており、多少前後するとはいえ平均から大きくそれる可能性は低いことを意味します。
そうです。まさにローリスク・ローリターンであると言えます。
そして反対にばらつきの大きい(標準偏差が大きい)グラフというものは、投資結果が平均から大きく外れる可能性が高いことを意味します。
こちらはまさにハイリスク・ハイリターンとなります。
これらは標準偏差の大きさ、いわゆる平均からのばらつき具合なのですが、ここでのポイントはこのばらつきの大きさとはプラス方向にもマイナス方向にも両方へのばらつきが大きいことを意味します。
そのため最初に挙げたように大きく利益を出したいのであれば、ばらつきの大きいものを選ばなくてはなりません。しかし、ばらつきが大きいものはプラスだけでなく、マイナス方向への変動も大きいため利益を得る可能性と同様に損をする可能性も大きくなります。
ここで冒頭に述べた結論に戻ってくるのですがまとめると、、、
いわゆるリスクとは投資で言うとリターンのばらつき具合を表しており、それはプラスにもマイナスにも価格のぶれる幅が大きいことを意味します。そしてそれは偏差値の例に挙げたように標準偏差という数字が大きければ大きいほどぶれ幅が大きいことを意味し、得をする可能性も損をする可能性も高いことを理解しそれを許容しなければなりません。
しかし同時にそれが意味することは、リスクとは見方を変えると単純に悪いものではなく、利益の源泉でもあると言えます。金融の世界ではこれを「ボラティリティ」ということもあります。そして投資などはいわゆるこのリスク部分のコントロールが非常に重要になると言われており、この管理方法や理論については追々書いていきたいなと思っています。
今回は少し長くなってしまいましたが、今日書いた「リスクとは標準偏差(ボラティリティ)のことである」ということを知っていると、のちに紹介したいリスク管理の方法の基礎について触れることができるため紹介させていただきました。


